Conversion Graphs
Conversion Graphs Revision
Conversion Graphs
Conversion graphs allow us to convert easily between units. They will all be straight line graphs with one unit on the the x-axis and the other on the y-axis. You will need to know how to use conversion graphs to convert units and potentially use them as part of a question.
Learning Objectives:
After this topic students will be able to:
- Use Conversion Graphs to convert between common units of measurement.
Conversion Graphs Method
When asked to convert units using conversion graphs, it is often useful to draw on the graph to help you.
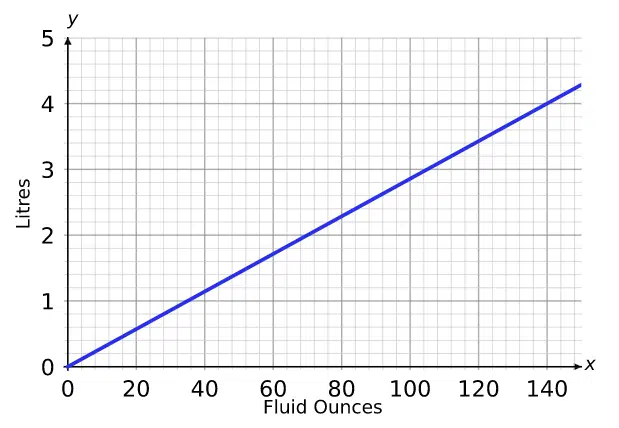
Example: The conversion graph shown is used for converting between litres and fluid ounces.
a) Convert \textcolor{limegreen}{2.5} litres into fluid ounces.
Step 1: On the y-axis start from \textcolor{limegreen}{2.5}, then draw a horizontal line until you meet the line.
Step 2: From this point, draw a vertical line downwards until it meets the x-axis.
Step 3: Read the value where the line meets the x-axis and this is the result of the conversion.
Using this method we can see that \textcolor{limegreen}{2.5} litres \approx \textcolor{limegreen}{88} fluid ounces.
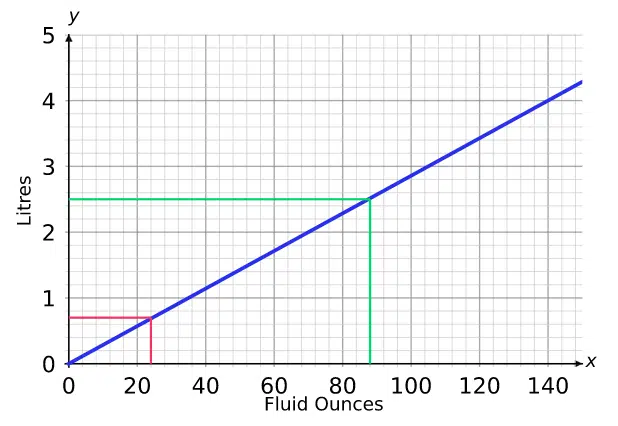
b) Convert \textcolor{red}{24} fluid ounces into litres.
Here, we have to reverse the process as we have to convert in the opposite direction: draw up to the line first, then across, and this time read off the result from the y-axis.
The \textcolor{red}{24} fluid ounce line finishes at round 0.7 on the y-axis.
So \textcolor{red}{24} fluid ounces \approx \textcolor{red}{0.7} litres.
Example: Conversion Graphs
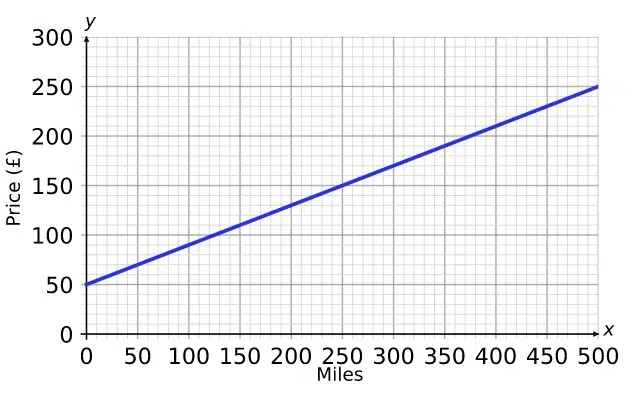
The relationship between miles driven and the price of a hire car is shown on the graph.
[2 marks]
a) Convert £100 into miles:
Draw a line from 100 on the y-axis to the blue line and then down to the x-axis. This gives a conversion of
\textcolor{limegreen}{£100} = \textcolor{limegreen}{125} miles
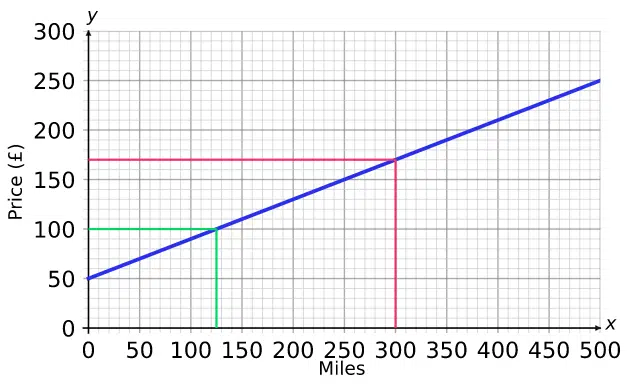
b) Convert 300 miles to £‘s:
Draw a line up from 300 on the x-axis to the conversion graph and then across to the y-axis. This gives a conversion of
\textcolor{red}{300} miles = \textcolor{red}{£170}
Conversion Graphs Example Questions
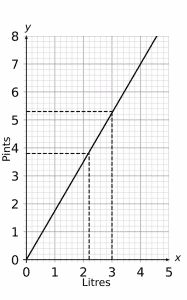
Question 1: Use the graph below to find an approximate value for the following conversions:
a) 3 litres to pints
b) 3.8 pints to litres
a) Converting litres to pints, draw a line vertically upwards from 3 on the horizontal (x) axis until it touches the black solid line of the graph. Then we need to draw a line from this point horizontally to the left to find the corresponding value on the vertical (y) axis. This value falls between 5.2 and 5.4 pints, so the approximate answer is
3 litres = 5.3 pints
b) Converting pints to litres, locate 3.8 on the vertical (y) axis and draw a line horizontally to the right until it touches the blue line of the graph. Then we need to draw a line from this point vertically down to find the corresponding value on the horizontal (x) axis. This value falls between 2 and 2.2 litres. Since it is closer to 2.2 than 2, the approximate answer is
3.8 pints =2.15 litres
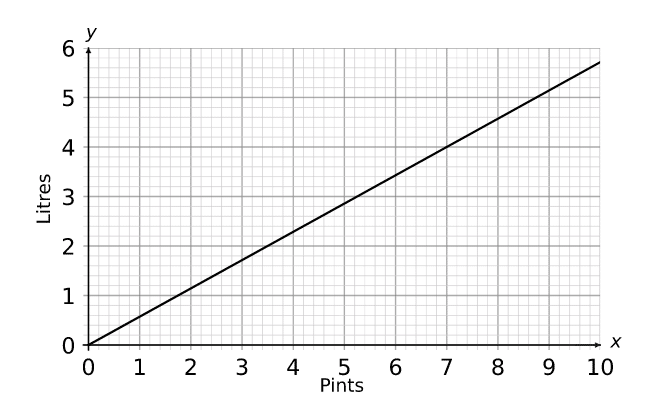
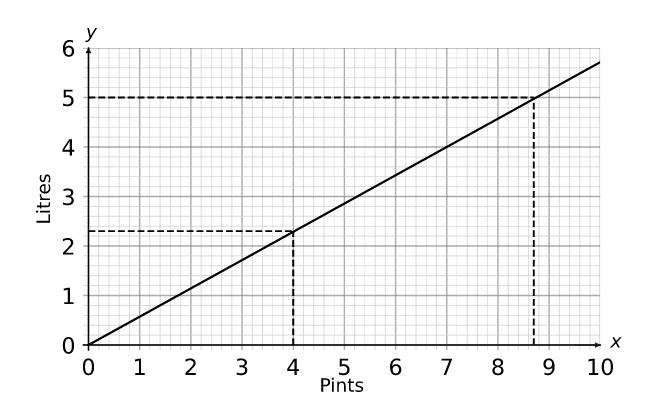
Question 2: Using the conversion graph find approximate values for:
a) The number of litres in 4 pints
b) The number of pints in 5 litres
a) First find 4 on the x axis and go up until you touch the line. Then go across to the corresponding value on the vertical y axis. We can see that this line touches between 2.2 litres and 2.4 litres, so we can say that
4 pints \approx 2.3 litres
b) Find 5 on the y axis and go across to the right until you touch the line. Then go down to the corresponding value on the horizontal x axis. We can see that this line touches between 8.6 pints and 8.8 pints so we can say that
5 litres \approx 8.7 pints
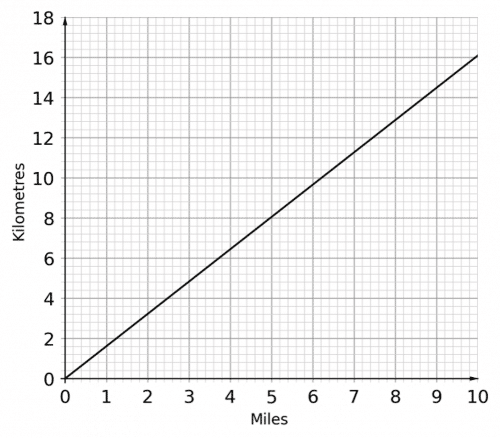
Question 3: Use the following conversion graph to convert 80 kilometres to miles.
8 km =5 miles
Therefore 80 km = 5 \times 10 = 50 miles