Revise

Fractions, Decimals and Percentages

Fractions, Decimals and Percentages Revision

Fractions, Decimals and Percentages

Here we will look at how to convert between fractions, decimals, and percentages. All 3 forms are equivalent ways of saying the same thing, but we normally use the one that is most appropriate in that particular scenario.

 

Learning Objectives:

After this topic students will be able to:

  • Convert between fractions, decimals and percentages.
  • Order and compare fractions, decimals and percentages.
Informational Image

Common Conversions

Fractions, decimals and percentages conversions are really useful to memorise.

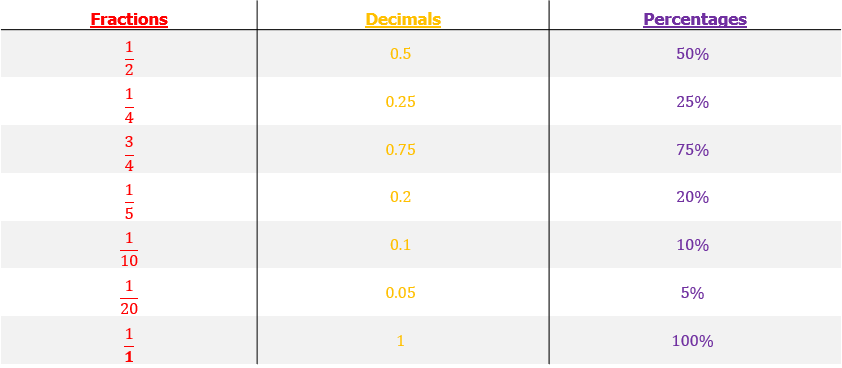
These are some common fractions, decimals and percentages you should remember.

Converting Fractions to Decimals to Percentages

Fractions to Decimals:

Treat the fraction like a division, so divide the top number of the fraction by the bottom number,

e.g. \dfrac{13}{20} = 13 \div 20 = 0.65

 

Decimals to Percentages:

Multiply the decimal by 100 (i.e. move the decimal point 2 places to the right) and add a \% sign,

e.g. 0.65 \times 100 = 65\%

Note: Convert fractions to percentages by converting the fraction to a decimal and then the decimal to a percentage

e.g. \dfrac{65}{100} = 0.65 = 65\%

Informational Image

Converting Percentages to Decimals to Fractions

Percentages to Decimals:

Divide by 100 (i.e. move the decimal point 2 places to the left) and remove the \% sign,

e.g. 65\% \div 100 = 0.65

 

Decimals to Fractions:

Write the decimal as a fraction with 1 on the bottom. Then, repeatedly multiply the top and the bottom of the fraction by 10 until the top number turns into a whole number,

e.g. 0.65 = \dfrac{0.65}{1} = \dfrac{6.5}{10} = \dfrac{65}{100}

Then, you can simplify the fraction if needed: \dfrac{65}{100} = \dfrac{13}{20}

Note: To convert straight from percentages to fractions, write the percentage as a fraction with 100 on the bottom, without the \% sign, and then simplify it

e.g. 65\% = \dfrac{65}{100} = \dfrac{13}{20}

Comparing Fractions, Decimals and Percentages

You will need to be able to compare and order fractions, decimals and percentages.

Example:  Put the following in order from smallest to largest:

23\%          \dfrac{1}{4}          \dfrac{6}{25}          0.245

Step 1: Convert all of the numbers into the same form (converting all to decimals is usually the easiest):

23\% = 0.23

\dfrac{1}{4} = 0.25

\dfrac{6}{25} = 0.24

Step 2: Rewrite the list as decimals:

0.23          0.25          0.24          0.245

Step 3: Put the list in order from smallest to largest, using the technique of ordering decimals:

0.23          0.24          0.245          0.25

Step 4: Write down the order, converting the decimals back into their original form:

23\%          \dfrac{6}{25}          0.245          \dfrac{1}{4}

Informational Image

Fractions, Decimals and Percentages Example Questions

Question 1: Write 19.4\% as a decimal.

Divide by 100 and remove the \% sign:

 

19.4\%\div100=0.194

Question 2: Write 0.712 as a fraction in its simplest form.

Write this decimal as a fraction with 1 on the bottom:

 

0.712=\dfrac{0.712}{1}

 

Make the numbers whole by multiplying the top and bottom of the fraction by 1000:

 

\dfrac{0.712 \times 1000}{1 \times 1000}=\dfrac{712}{1000}

 

Finally, simplify the fraction fully:

 

\dfrac{712}{1000}=\dfrac{89}{125}

Question 3: Write the following in order from largest to smallest:

 

\dfrac{1}{2}          \dfrac{13}{25}           0.51          51.2\%

Convert all of the numbers into decimals:

 

\dfrac{1}{2} = 0.5

 

\dfrac{13}{25} = 0.52

 

51.2\% = 0.512

 

Rewrite the list as decimals:

 

0.5          0.52          0.51          0.512

 

Put the list in order from largest to smallest, using the technique of ordering decimals:

 

0.52          0.512          0.51          0.5

 

Write down the order, converting the decimals back into their original form:

 

\dfrac{13}{25}          51.2\%          0.51          \dfrac{1}{2}