Problems Involving Money

Rate of Pay

The rate of pay is the cost of something per unit of time, for example a phone call may cost $25$p per minute or someone may get paid $£11.70$ per hour.

Often questions require you to combine a rate of pay with a fixed fee, or combine two different rates of pay.

Example 1: Sarah earns $\textcolor{red}{£9.80}$ per hour and works $\textcolor{limegreen}{30}$ hours in one week. She earned $\textcolor{red}{£32.50}$ in tips.

How much did she earn in the week?

First calculate how much she earns from her hourly rate of pay: $\textcolor{limegreen}{30}\times \textcolor{red}{£9.80}=£294$

Then calculate her total earnings for the week: $£294+\textcolor{red}{£32.50}=\textcolor{black}{£326.50}$

Example 2: Stephen wants to re-tile his bathroom and also replace his shower.

A tiler charges $\textcolor{red}{£24}$ per hour and says it will take $\textcolor{limegreen}{11}$ hours work.

A plumber charges $\textcolor{red}{£28.50}$ per hour and says it will take $\textcolor{limegreen}{9}$ hours to fit the work.

How much will it cost Stephen in total to do both jobs?

Cost of re-tiling his bathroom: $\textcolor{red}{£24} \times \textcolor{limegreen}{11}=£264$

Cost of replacing his shower: $\textcolor{red}{£28.50} \times \textcolor{limegreen}{9}=£256.50$

Total Cost: $£264+£256.50=\textcolor{black}{£520.50}$

Discounts and Increases as Percentages

Often questions ask you to find the new price of an item after it has been increased or discounted by a certain percentage.

Price Decrease

If a product’s price has been reduced by a percentage, we take this value away from $100\%$ and then convert this value into a decimal to then multiply it by the original price.

Example 1: A pair of trainers costs $\textcolor{orange}{£45}$. If there is a sale on which gives $\textcolor{blue}{20\%}$ off the price, what will be the new price of the trainers?

New price of the trainers: $\textcolor{orange}{£45}\times0.8=\textcolor{black}{£36}$

Price Increase

If a product’s price has been increased by a percentage, we add this value to $100\%$ and then convert this value into a decimal to then multiply it by the original price.

Example 2: Lucy bought a house for $\textcolor{orange}{£210000}$ last year, she has the house valued $1$ year later and is told that the value of the house has increased by $\textcolor{blue}{10\%}$. Calculate the new value of the house.

$100\%+10\%=110\%=1.1$

New value of house: $1.1 \times \textcolor{orange}{£210000}=\textcolor{black}{£231000}$

Note: Alternatively, we could have found what $10\%$ of $£210000$ was and then added this to the original value of the house.

Discounts as Fractions

You could also be asked to find the new price of an item after a discount in terms of a fraction has been applied.

It’s important to be comfortable with fractions when attempting this style of question.

Example: A bike costs $\textcolor{orange}{£330}$. If there is a sale on which gives $\textcolor{blue}{\dfrac{2}{5}}$ off the price, what will be the new price of the bike?

First, calculate $\dfrac{2}{5}$ of the original price:

$2 \div 5 \times \textcolor{orange}{£330} = £132$

Then, subtract this from the original price of the bike:

$\textcolor{orange}{£330} - £132 = \textcolor{black}{£198}$

Percentage Profit

Percentage profit is the profit of selling an item as a percentage of the total costs involved.

$\text{\textcolor{purple}{Profit}} = \text{\textcolor{blue}{Selling Price}} - \text{\textcolor{red}{Costs}}$

$\textcolor{limegreen}{\% \text{ Profit}}=\dfrac{\text{\textcolor{purple}{Profit}}}{\text{\textcolor{red}{Costs}}}\times100$

Example: Gareth buys an old car for $£1250$, he then buys some replacement parts for $£250$. He sells the car on for $£2100$, calculate his percentage profit.

Profit $=£2100-(£1250+£250)=£600$

$\%$ Profit $=\dfrac{600}{1500}\times100=40\%$

Best Buys Method

When answering best buy questions, to find which deal is the best value for money we have to calculate the value of each product for a common amount.

Example: Three different brands of washing powder are on sale. Their prices are shown below.

Work out which brand provides the best value for money.

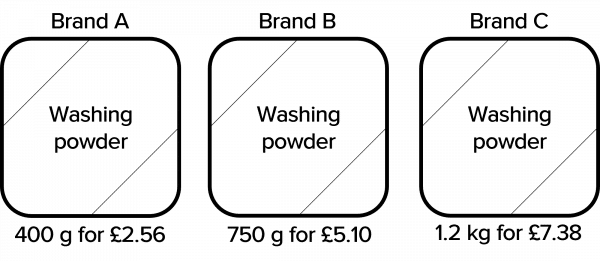
To compare the prices of the different brands we will work out how much it costs to buy $100$ g of each brand, then we will be able to see which brand is the most cost effective.

Brand A: The price shown is for $400$ g, so if we divide the value by $4$, we get

$\text{\textcolor{blue}{Brand A cost of 100 g }}=2.56\div 4= \textcolor{blue}{\pounds 0.64}$

Brand B: The price shown is for $750$ g, so this time we want to divide the value by $7.5$,

$\text{\textcolor{red}{Brand B cost of 100 g }}=5.10\div 7.5= \textcolor{red}{\pounds 0.68}$

Brand C: The price shown is for $1.2$ kg, which is the same as $1200$ g, so we divide by $12$,

$\text{\textcolor{darkorange}{Brand C cost of 100 g }}=7.38\div 12= \textcolor{darkorange}{\pounds 0.615}$

Comparing the $3$ values, we can see that the cheapest price per $100$ g is Brand C.

Note:  Whilst you can’t actually have $£0.615$ (because that would involve having half a penny), it’s okay to use that value to compare prices in a best buy questions.