Ratio
Ratio Revision
Ratio
A ratio is something we use to compare how much there is of one thing to how much there is of another.
A ratio is written like 2:5 and is spoken as “2 to 5”. This means that for every 2 lots of one thing, there must be 5 lots of the other.
Learning Objectives:
After this topic students will be able to:
- Simplify given ratios
- Work out individual and total amounts from given ratios
- Use ratios in real life contexts
Simplifying Ratios
To simplify a ratio, divide each part of the ratio by the same number each time, until they can no longer be divided.
Example: Write the ratio \textcolor{red}{18}:\textcolor{blue}{60}:\textcolor{limegreen}{24} in its simplest form.
We can divide each number by 3 and then by 2 (or just by 6):
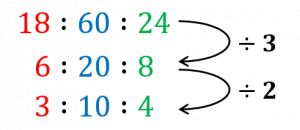
This cannot be simplified anymore to make whole numbers, so the ratio is in its simplest form, which is \textcolor{red}{3}:\textcolor{blue}{10}:\textcolor{limegreen}{4}
Solving Questions Involving Ratios
There are various types of questions involving ratios that you will encounter.
Example 1: Olive makes her tea by adding \textcolor{blue}{1} part milk to \textcolor{red}{7} parts hot water (\textcolor{blue}{1} : \textcolor{red}{7}). If Olive uses 30 ml of milk, how much hot water does she use?
The amount of milk used is \text{\textcolor{blue}{1 part}} = \textcolor{blue}{30 \text{ ml}}
Olive uses 7 parts of hot water to every part of milk.
So,
The amount of hot water used is \textcolor{red}{\text{7 parts}} = \textcolor{red}{7} \times \textcolor{blue}{30} = \textcolor{black}{210 \text{ ml}}
Example 2: Simon and Luca sell some items at an auction. They make £450 in total.
They split the money they make respectively in the ratio \textcolor{red}{4}:\textcolor{limegreen}{5}. Work out how much money each of them receive.
The ratio tells us that there are
\textcolor{red}{4} + \textcolor{limegreen}{5} = 9 parts
\textcolor{red}{4} of these go to Simon and \textcolor{limegreen}{5} of these go to Luca.
So, find how much \textcolor{purple}{1} part of £450 is worth, by dividing the total number of parts, 9
\textcolor{purple}{\text{1 part}} = £450 \div 9 = \textcolor{purple}{£50}
So,
\text{Simon's share} = \textcolor{red}{4 \text{ parts}} = \textcolor{red}{4} \times \textcolor{purple}{£50} = \textcolor{black}{£200}
\text{Luca's share} = \textcolor{limegreen}{5 \text{ parts}} = \textcolor{limegreen}{5} \times \textcolor{purple}{£50} = \textcolor{black}{£250}
Calculating Total Amounts
You can use ratios to calculate total amounts, using the following steps:
Step 1: Calculate the value of one part (you may be given this in the question).
Step 2: Calculate the total number of parts.
Step 3: Calculate the total amount, by multiplying the value of one part by the total number of parts.
Example: A basic dough is made by mixing \textcolor{blue}{3} parts of Greek yoghurt and \textcolor{limegreen}{4} parts self-raising flour.
160 g of self-raising flour is used. How much dough is made in total?
4 parts self-raising flour is 160 g, so
\textcolor{purple}{\text{1 part}} = 160 \div 4 = \textcolor{purple}{40 \text{ g}}
The total number of parts is
\textcolor{blue}{3} + \textcolor{limegreen}{4} = \textcolor{red}{7}
So, the total amount of dough made is
\textcolor{red}{7} \times \textcolor{purple}{40 \text{ g}} = \textcolor{black}{280 \text{ g}}
Ratio Example Questions
Question 1: There are 160 men and 280 women in a crowd. What is the ratio of men to women, in its simplest form?
The ratio of men : women is 160 : 280
This can be simplified, by dividing both sides by 10:
16:28
it can be simplified further, by dividing both sides by 4:
4:7
This can no longer be divided to make whole numbers, so it is in its simplest form.
Question 2: Liam makes fruit squash by adding 5 parts of water to 1 part of squash. How much water would he used if he used 50 ml of squash?
The amount of squash used is 1 part = 50 ml
Liam uses 5 parts of water to every part of squash.
So, the amount of water needed is
5 \times 50 ml = 250 ml
Question 3: Adam, Ben and Charlie are three brothers. The brother’s ages added together is 63. The ratio of their ages is 3:4:2. How old is each brother?
The total number of parts in the ratio is
3 + 4 + 2 = 9
1 part is worth
63 \div 9 = 7 years
Adam’s part of the ratio is 3 parts, so he is
3 \times 7 = 21 years old
Ben’s part of the ratio is 4 parts, so he is
4 \times 7 = 28 years old
Charlie’s part of the ratio is 2 parts, so he is
2 \times 7 = 14 years old

