Unit Conversions
Unit Conversions Revision
Unit Conversions
All measurements need units, whether that’s length, weight or capacity. There are two main types of units, metric and imperial. You will also encounter other units. You will need to be able to convert between units to solve calculations.
Learning Objectives:
After this topic students will be able to:
- Identify common units of length, weight and capacity.
- Convert between metric and imperial units.
- Convert between different types of metric unit.
Common Units
The table below shows some common metric and imperial units for length, weight and capacity. The length of something is how long it is. The weight of something is how heavy it is. The capacity of something is how much it can hold.
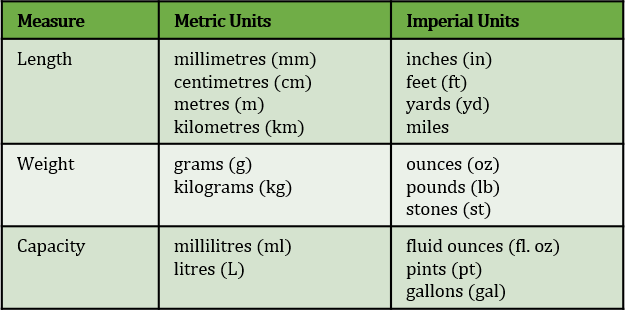
Metric and Imperial Unit Conversions
You will need to know the conversion factor to go between metric and imperial units, to then multiply or divide by this value to convert the unit.
The tables below show some common metric and imperial unit conversions. You only need to memorise the metric conversions, if you have to convert imperial units you’ll be told the conversion factor.

You can convert between any units as long as you are given (or know) the conversion factor.
Unit Conversions – Metric and Money
Converting Metric units is very simple, all we need to do is multiply or divide similar units by a conversion factor
Example 1: Converting from \text{kg} to \text{g} and vice versa:
3\text{ kg} = 3 \times 1000 = 3000\text{ g}
3000\text{ g} = 3000\div 1000 = 3\text{ kg}
Example 2: Converting from Pounds (£) to pence (p) and vice versa:
£3.50 = 3.5 \times 100 = 350p
350p = 350\div 100 = £3.50
Unit Conversions – Volume
There are different ways the units of volume can be written:
\begin{aligned} \textcolor{red}{1 \text{ cm}^3} &= \textcolor{red}{1 \text{ ml}} \\ \textcolor{blue}{1 \text{ m}^3} &= \textcolor{blue}{1000 \text{ L}} \end{aligned}
You may be given questions where you have to convert between these, but you will be given these in the question.
Example 1: Metric to Imperial Conversion
Frazer buys a bag of soil for his garden that has a mass of 15.2 kg. What is the mass of the bag of soil in pounds to 1 decimal place?
Use the conversion rate 1 pound = 0.4536\text{ kg}.
[1 mark]
To convert from kilograms to pounds we need to divide by 0.4536
\text{Mass of bag of soil} = 15.2\div 0.4536 = 33.5 pounds (1 decimal place)
Example 2: Money Conversion
Sanjay paid \$400 for a hotel stay. How much is this in pounds (£)?
£1 = \$1.25[1 mark]
400 \div 1.25= 320
So, Sanjay paid £320 for the hotel stay.
Example 3: Volume Conversion
Shavaughn has a measuring cylinder with a capacity of 250 cm^3. She pours water into the cylinder, and stops when the water takes up half of the measuring cylinder’s capacity.
What volume of water did Shavaughn pour into the measuring cylinder? Give your answer in millilitres.
Use 1 cm^3 =1 ml
[1 mark]
250 \div 2=125 cm^3
125 cm^3 = 125 ml
Unit Conversions Example Questions
Question 1: Kerry is going on holiday to Spain and needs to convert £400 into euros. There is a 2\% fee for converting the currency.
Using the conversion rate: \pounds 1 = €1.17, calculate how many euros she will be able to take on holiday.
[1 mark]
We can either deduct the 2\% commission from the amount in pounds at the start or from the amount in euros at the end.
A 2\% decrease means she will have 98\% of her money left over, so
\text{Money left } = \dfrac{98}{100} \times 400 = \pounds 392
Using the conversion rate given in the question, we can find out how much £392 is in euros.
392\times 1.17 = €458.64
Question 2: Meghan goes on a 3.1 kilometre walk with her dog. What is the distance of Meghan’s walk in feet, to the nearest foot?
Use the conversion rate: 1\text{ foot} = 0.3048\text{ metres}.
[1 mark]
The conversion rate is between metres and feet, so first we need to convert 3.1km into metres. We know that 1km is 1000m, so:
3.1\text{km} = 3.1 \times 1000 \text{m} = 3100\text{m}
If 1 foot is equal to 0.3048 metres, that means we would have to multiply a distance in feet by 0.3048 in order to get the equivalent distance in metres. So, to go from metres to feet, we will have to divide by 0.3048. This means Meghan’s walk in feet is:
3100 \text{ metres} \div 0.3048 \text{ metres}= 10171\text{ feet} (to nearest foot)}
Question 3: Declan has bought a container that measures 90\text{ cm} \times 130\text{ cm} \times 110\text{ cm}. What is the volume of his container in litres?
1 m^3 = 1000 L
[1 mark]
Converting the measurements from cm to m first:
90 cm = 0.9 m
130 cm = 1.3 m
110 cm = 1.1 m
Then calculate the volume of the container in m^3:
0.9\times1.3\times1.1=1.287 m^3
Finally, convert to litres:
1.287 m^3 = 1287 L

